向聴数を求めるプログラム(修正版)

麻雀の副露判断アルゴリズム(2) - koba::blog で「特定の役への向聴数」を計算する方法を導入したが、バグがあるようである。例えば下記の2つの牌姿の(索子の)混一色への向聴数は

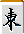
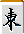
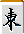
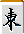
2向聴
3向聴

であるが、ともに2面子2搭子のため、同一の向聴数と判定してしまう。

向聴数を求める公式

上記の2つの牌姿は孤立牌の有無により向聴数が異なるのだが、現在のアルゴリズムはよく知られている公式にしたがい

向聴数＝ 8 ー面子の数 × 2 ー搭子の数

としており、孤立牌を計算に含めていない。この公式は牌が13枚に満たない場合を想定しておらず、このような状況では使うことができなかったのだ*1。そもそも牌が0枚の場合は13向聴のはずである。例えば、

は国士無双の聴牌だが、断幺九では13向聴となる。

牌の枚数に関わらず成り立つ公式は、孤立牌の数も計算式に含めた

向聴数＝ 13 ー面子の数 × 3 ー搭子の数 × 2 ー孤立牌の数
(ただし) 面子の数＋搭子の数＋孤立牌の数 ≦ 5

となる。

牌が13枚もしくは14枚の場合は常に「面子の数＋搭子の数＋孤立牌の数 ≧ 5」*2となるため、これを利用して簡略化したものが元の公式だったのである*3。

七対子の向聴数も同様に

向聴数＝ 13 ー対子の数 × 2 ー孤立牌の数
(ただし) 対子の数＋孤立牌の数 ≦ 7

が牌の枚数に関わらない向聴数を求める公式となる。

修正プログラム

まず新しい公式の関数を用意する。

function _xiangting(m, d, g, j) {

    var n = j ? 4 : 5;  // 雀頭がない場合は5ブロック必要
    if (m         > 4) { d += m     - 4; m = 4         }  // 面子過多の補正
    if (m + d     > 4) { g += m + d - 4; d = 4 - m     }  // 搭子過多の補正
    if (m + d + g > n) {                 g = n - m - d }  // 孤立牌過多の補正
    if (j) d++;         // 雀頭がある場合は搭子として数える
    return 13 - m * 3 - d * 2 - g;
}

m: 面子の数
d: 搭子の数(雀頭は含めない)
g: 孤立牌の数
j: 雀頭があるとき真

冒頭の例に適用すると、1.は m = 2, d = 2, g = 1, j = false なので2向聴、2.は m = 2, d = 2, g = 0, j = false なので3向聴となる。

次に搭子の数を求める関数で孤立牌の数(n_guli)も求めるよう修正する。

function dazi(bingpai) {

    var n_pai  = 0, n_dazi = 0, n_guli = 0;

    for (var n = 1; n <= 9; n++) {
        n_pai += bingpai[n];
        if (n <= 7 && bingpai[n+1] == 0 && bingpai[n+2] == 0) {
            n_dazi += n_pai >> 1;
            n_guli += n_pai  % 2;
            n_pai = 0;
        }
    }
    n_dazi += n_pai >> 1;
    n_guli += n_pai  % 2;

    return [ [ 0, n_dazi, n_guli ],
             [ 0, n_dazi, n_guli ] ];
}

面子でも搭子でもない牌が孤立牌である。上記関数は面子の抜き取りが終わった後に呼ばれるので、搭子としなかった牌は孤立牌となる。

面子を抜き取る関数はほぼ修正なし。

function mianzi(bingpai, n) {

    if (n > 9) return dazi(bingpai);    // 関数dazi()の返り値を変えたので修正

    var max = mianzi(bingpai, n+1);
    
    if (n <= 7 && bingpai[n] > 0 && bingpai[n+1] > 0 && bingpai[n+2] > 0) {
        bingpai[n]--; bingpai[n+1]--; bingpai[n+2]--;
        var r = mianzi(bingpai, n);
        bingpai[n]++; bingpai[n+1]++; bingpai[n+2]++;
        r[0][0]++; r[1][0]++
        if (r[0][0]* 2 + r[0][1] > max[0][0]* 2 + max[0][1]) max[0] = r[0];
        if (r[1][0]*10 + r[1][1] > max[1][0]*10 + max[1][1]) max[1] = r[1];
    }
    
    if (bingpai[n] >= 3) {
        bingpai[n] -= 3;
        var r = mianzi(bingpai, n);
        bingpai[n] += 3;
        r[0][0]++; r[1][0]++
        if (r[0][0]* 2 + r[0][1] > max[0][0]* 2 + max[0][1]) max[0] = r[0];
        if (r[1][0]*10 + r[1][1] > max[1][0]*10 + max[1][1]) max[1] = r[1];
    }
    
    return max;
}

面子数、搭子数、孤立牌数が確定した後は、今まで行っていた少牌の補正、面子・搭子過多の補正、雀頭有無の補正がすべて不要となる。

function mianzi_all(shoupai, jiangpai) {

    var r = {};
    
    r.m = mianzi(shoupai._bingpai.m ,1);
    r.p = mianzi(shoupai._bingpai.p ,1);
    r.s = mianzi(shoupai._bingpai.s ,1);

    var z = [0, 0, 0];
    for (var n = 1; n <=7; n++) {
        if (shoupai._bingpai.z[n] >= 3) z[0]++;
        if (shoupai._bingpai.z[n] == 2) z[1]++;
        if (shoupai._bingpai.z[n] == 1) z[2]++; // 字牌の孤立牌数取得を追加
    }

    var n_fulou = shoupai._fulou.length;

    var min_xiangting = 13;                     // 向聴数の初期値を8から13に変更

    for (var m of r.m) {
        for (var p of r.p) {
            for (var s of r.s) {
                var n_mianzi = m[0] + p[0] + s[0] + z[0] + n_fulou;
                var n_dazi   = m[1] + p[1] + s[1] + z[1];
                var n_guli   = m[2] + p[2] + s[2] + z[2];
                var xiangting = _xiangting(n_mianzi, n_dazi, n_guli, jiangpai);
                                                 // 面子・搭子過多の補正を削除
                if (xiangting < min_xiangting) min_xiangting = xiangting;
            }
        }
    }

    return min_xiangting;
}

function xiangting_yiban(shoupai) {

    var min_xiangting = mianzi_all(shoupai);    // 少牌の場合の補正を削除

    for (var s of ['m','p','s','z']) {
        for (var n = 1; n <= shoupai._bingpai[s].length; n++) {
            if (shoupai._bingpai[s][n] >= 2) {
                shoupai._bingpai[s][n] -= 2;
                var xiangting = mianzi_all(shoupai, true);
                                                // 雀頭ありの場合の補正を削除
                shoupai._bingpai[s][n] += 2;
                if (xiangting < min_xiangting) min_xiangting = xiangting;
            }
        }
    }
    
    return min_xiangting;
}

七対子の向聴数を求める関数も新しい公式にしたがうよう修正する。

function xiangting_qiduizi(shoupai) {

    var n_duizi = 0;
    var n_danqi = 0;
    
    for (var s of ['m','p','s','z']) {
        var bingpai = shoupai._bingpai[s];
        for (var n = 1; n < bingpai.length; n++) {
            if      (bingpai[n] >= 2) n_duizi++;
            else if (bingpai[n] == 1) n_danqi++;
        }
    }

    if (n_duizi           > 7) n_duizi = 7;             // 対子過多の補正
    if (n_duizi + n_danqi > 7) n_danqi = 7 - n_duizi;   // 孤立牌過多の補正

    return 13 - n_duizi * 2 - n_danqi;              // 向聴数の初期値を13とし、
                                                    // 孤立牌数も計算に追加
}

全体の修正箇所は以下の通り。

#25 少牌・多牌の場合の向聴数計算が誤っているバグを修正 · kobalab/Majiang@0ca5a6f

*1:麻雀の副露判断アルゴリズム(2) - koba::blog で補正しているが補正方法が不十分

*2:つまり常に5ブロックの元があるということ

*3:13 ー面子の数 × 2 ー搭子の数ー (面子の数＋搭子の数＋孤立牌の数) → 8 ー面子の数 × 2 ー搭子の数