麻雀の役を判定をするときには、まず和了形を求める必要がある。
例えば上記の牌姿の場合は、以下の2つの和了形が存在する。
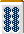
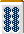
(三暗刻)- (純全帯幺九＋一盃口)
このように和了形が複数あるときは和了点の高い方を採用する*1ので、全ての和了形をもれなく求める必要がある。そのためには バックトラック法 と呼ばれる手法を用いるのが一般的だ。ところがネット上で見かける和了形を求めるアルゴリズムは「アドホックな解法」ばかりでバックトラックを説明したものが見当たらない*2。ならばということで、本稿で説明することにした。
和了形を求める手順
4面子1雀頭形の場合*3、和了形を求める手順は以下となる。
- 2枚以上ある牌を雀頭候補として抜き取る
- 残った12枚から4面子となる組合せをすべて求める
- 和了牌を4面子1雀頭のどれに含めるか決定する
このそれぞれに複数の選択があり得るため、和了形が複数求まることがある。
(1) 雀頭はどれか
雀頭を とするか(平和)、 とするか(三色同順)。
(2) 順子か刻子か
冒頭で紹介した形。萬子を順子とするか(純全帯幺九＋一盃口)、刻子とするか(三暗刻)。
(3) 待ちは何か
を両面待ちとするか(40符)、嵌張待ちとするか(50符)。
バックトラック法を用いるのは 2. 残った12枚から4面子となる組合せをすべて求める の部分なので、これについて説明する。面子は色をまたがることはないので、萬・筒・索子、字牌についてそれぞれ調べればよい。問題となるのは刻子・順子がともに現れる数牌なので、数牌について考える。
アドホックな解法
麻雀の和了形を求めるアルゴリズムの証明 #アルゴリズム - Qiita などで説明されている方法*4。
- 刻子をいくつか抜き、残りを全て順子として抜く
冒頭に示した手牌の場合は、萬子の に対して、
- 1, 2, 3 いずれも刻子として抜く
- 刻子を一切抜かない
の2種類が解となる。
の場合、刻子は 1, 3, 4 の3つあるが、
- 1 のみを刻子として抜く
のみが解となる。
牌が12枚の場合、刻子は最大で4つある可能性があるので、そのそれぞれについて 抜く・抜かない の2通り、つまり 2 x 2 x 2 x 2 = 16 通りを試せばよい。実際には、①刻子を抜かない、②最初の刻子のみ抜く、③最後の刻子のみ抜く、④全ての刻子を抜く の4通りを試すだけでよいとのことである*5。
バックトラックによる解法
電脳麻将 の GitHub - kobalab/majiang-core: 麻雀基本ライブラリ で使用している方法。
- 刻子として使う・使わないを 再帰的に 全てのパターンについて試みる
プログラムは以下としている。
function mianzi(s, bingpai, n = 1) { if (n > 9) return [[]]; /* 面子をすべて抜き取ったら次の位置に進む */ if (bingpai[n] == 0) return mianzi(s, bingpai, n+1); /* 順子を抜き取る */ let shunzi = []; if (n <= 7 && bingpai[n] > 0 && bingpai[n+1] > 0 && bingpai[n+2] > 0) { bingpai[n]--; bingpai[n+1]--; bingpai[n+2]--; shunzi = mianzi(s, bingpai, n); // 抜き取ったら同じ位置で再試行する bingpai[n]++; bingpai[n+1]++; bingpai[n+2]++; for (let s_mianzi of shunzi) { // 試行結果のすべてに抜いた順子を加える s_mianzi.unshift(s+(n)+(n+1)+(n+2)); } } /* 刻子を抜き取る */ let kezi = []; if (bingpai[n] == 3) { bingpai[n] -= 3; kezi = mianzi(s, bingpai, n+1); // 抜き取ったら次の位置に進む bingpai[n] += 3; for (let k_mianzi of kezi) { // 試行結果のすべてに抜いた刻子を加える k_mianzi.unshift(s+n+n+n); } } /* 順子のパターンとと刻子のパターンをマージしてすべて返す */ return shunzi.concat(kezi); }
バックトラック法は再帰アルゴリズムであり、mianzi() はその中で再度 mianzi() を呼び出す 再帰関数 となっている。冒頭に示した例の場合は、mianzi('m', [0,3,3,3,0,0,0,0,0,0]) を実行すればよい*6。すると以下のように探索が行われ*7、解が求まる。
- 123 を抜く。
- 再度 123 を抜く。
- 再度 123 を抜く。
- 123, 123, 123 が解として得られる。
- 1 にバックトラックして刻子を試す。
- 111 を抜き、2 に進む。
- 222 を抜き、3 に進む。
- 333 を抜く。
- 111, 222, 333 が2つ目の解として得られる。
2つ目の例の場合は、mianzi('m', [0,3,1,3,3,2,0,0,0,0]) の実行で、以下のように探索が行われる。
- 123 を抜く。
- 再度 123 を抜こうとするが、2 がないので失敗し、バックトラックする。
- 111 を抜き、2 に進む。
- 234 を抜き、3 に進む。
- 345 を抜く。
- 再度 345 を抜く。
- 111, 234, 345, 345 が解として得られる。
先頭から探索を行っているので 333 や 444 を試さず探索が完了する。このようにバックトラック法では無駄なく少ない試行で解を求めることができる。
再帰アルゴリズムは難易度が高いのでアドホックなやり方に逃げがちになるが「競プロ」では定番の手法になっているはずである*8。ここで紹介した和了形を求めるアルゴリズムを含め、麻雀アプリ作成に必要なアルゴリズムについては以下の書籍で解説したので、興味ある方は手にとっていただければ幸いである。
